백준 2609번 "최대공약수와 최소공배수"

Question:

두 개의 자연수를 입력받아
최대 공약수와 최소 공배수를 출력하는 프로그램을 작성하시오.

Input:

첫째 줄에는 두 개의 자연수가 주어진다.
이 둘은 10,000이하의 자연수이며 사이에 한 칸의 공백이 주어진다.

Output:

첫째 줄에는 입력으로 주어진 두 수의 최대공약수를,
둘째 줄에는 입력으로 주어진 두 수의 최소 공배수를 출력한다.

Restriction:

시간제한:
1초

Example Case:

Input case:
24 18

Output case:
6
72

풀이 과정:

이 문제는 “유클리드 호제법” 알고리즘을 활용한 문제이다.

“유클리드 호제법(Euclidean Algorithm)” 이란,
두 양의 정수-혹은 두 다항식의 최대공약수를 구하는 방법이다.

두 양의 정수 a,b(a > b)에 대하여
a = bq + r(0 <= r < b)라 하면,
a,b의 최대공약수는
b,r의 최대공약수와 같다.
gcd(a,b) = gcd(b,r)
r = 0이라면, a,b의 최대공약수는 b가 된다.

이를 증명하면,

gcd(a,b) = G라 하자.
그럼 서로소인 정수 A, B에 대해
a = GA,b = GB가 성립한다.
이를 앞선 식 a = bq + r 에 대입하면,
GA = GBq + r이고, r = G(A-Bq)이다.
여기서 G는 b와 r의 공약수이고
만약 B와 A - Bq가 서로소
즉 gcd(B, A-Bq) = 1이면
gcd(b,r) = G이므로 증명이 된다.

이 유클리드 호제법은,
위 성질을 여러번 사용하여
보통 나머지가 0이 될 때까지 사용한다.

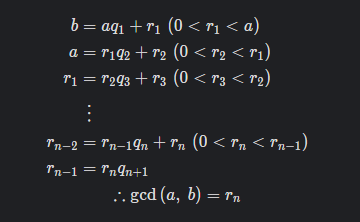
위의 공식처럼,
예시를 들자면

12345 = 1234 * 10 + 5
1234 = 5 * 246 + 4
5 = 4 * 1 + 1
4 = 1 * 4
gcd(12345, 1234) = 1

…따라서 12345와 1234의 최대공약수는 1이다.

아래는 python으로 작성한 코드이다.

def Euclidean(a,b):
    while b != 0:
        r = a % b
        a = b
        b = r
    return a

A,B = map(int,input().split())
print(Euclidean(A,B))
print(A*B // Euclidean(A,B)) #최소공배수는 A*B를 최대공약수로 나누자.

#plus
이 알고리즘은 인류 최초의 알고리즘이라 한다.

• 백준
• 문제풀이