백준 2805번 "나무 자르기"

22 Aug 2021 ~ 22 Jul 2020

Question:

상근이는 나무 M미터가 필요하다.
근처에 나무를 구입할 곳이 모두 망해버렸기 때문에,
정부에 벌목 허가를 요청했다.
정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고,
상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할것이다.

목재절단기는 다음과 같이 동작한다.
먼저,상근이는 절단기에 높이 H를 지정해야 한다.
높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다.
그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다.
따라서,높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고,
낮은 나무는 잘리지 않을 것이다.
예를 들어,
한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자.
상근이가 높이를 15로 지정했다면,
나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고,
상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다.
(총 7미터를 집에 들고 간다)
절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.

상근이는 환경에 매우 관심이 많기 때문에,
나무를 필요한 만큼만 집으로 가져가려고 한다.
이때,적어도 M미터의 나무를 집에 가져가기 위해서
절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.

Input:

첫째 줄에 나무의 수 N과
상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다.
(1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)

둘째 줄에는 나무의 높이가 주어진다.
나무의 높이의 합은 항상 M보다 크거나 같기 때문에,
상근이는 집에 필요한 나무를 항상 가져갈 수 있다.
높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.

Output:

적어도 M미터의 나무를 집에 가져가기 위해서
절단기에 설정할 수 있는 높이의 최댓값을 출력한다.

Restriction:

시간제한:
1 초

Example Case: Input case 1:

4 7
20 15 10 17

Output case 1:

Input case 2:

5 20
4 42 40 26 46

Output case 2:

풀이 과정: 이 문제는,
Parametric Search 알고리즘을 활용한 문제이다.

“PARAMETRIC SEARCH”란?
파라메트릭 서치는 이분 탐색법과 매우 유사한 알고리즘이다.
간단하게 정의를 내리면,
최적화 문제를 결정 문제로 바꾸어 푸는 알고리즘이다.

예시를 들어보자,
10명의 후보자가 나이순(오름차순)으로 정렬되있는 상황을 가정한다.
이중에서 합법적으로 주류를 구매 가능한 가장 어린 사람을 찾고자 한다.
이 상황도
“주류를 구매 가능한 가장 어린” 후보자를 찾는게 목표이다.(최적화)
최적화 문제임을 알았으니 후보자들을 대상으로
결정문제로 바꾸어 보자.

“주류를 구매 가능한 나이인가요?”

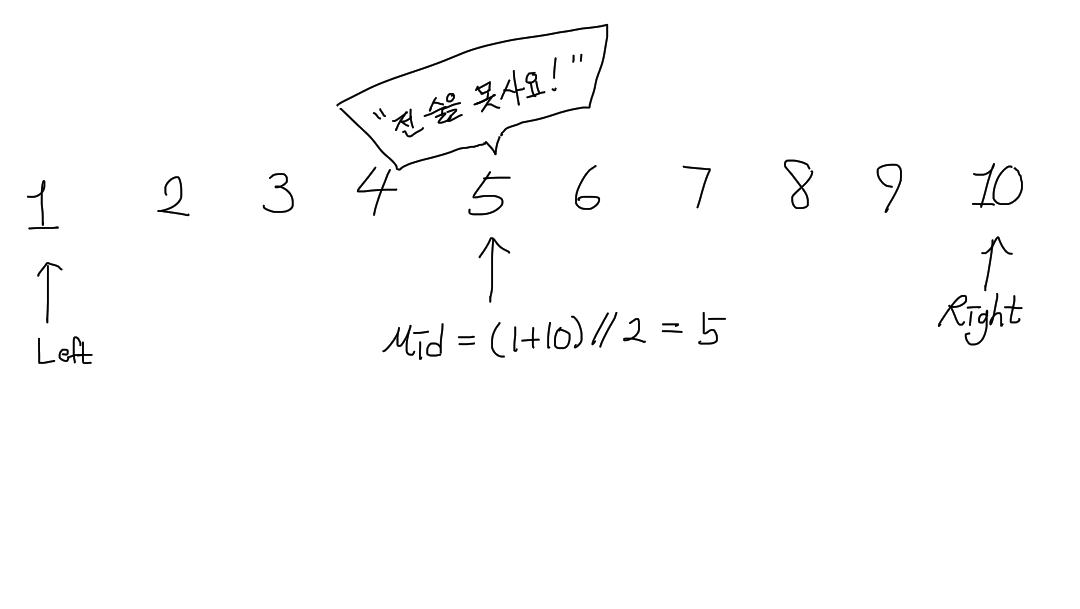
10명의 원소(*후보자)중,
left,right,mid 포인터를 이용하여 파라매트릭 서치를 진행해보자.

우선,
mid 포인터가 가리키는 원소에 대해
“주류를 구매 가능한 나이인가요?”라는 물음에 대한 결정으로,

성립하면 정답 범위는 오름차순 정렬에 따른 원소로 인해
mid(5)이상의 원소는 전부 정답범위에 들어가게 된다.
따라서 범위 감축을 위해 mid값보다 앞 원소의 정답 여부를 확인해야한다.
(right = mid - 1)

만일 성립하지 않게 된다면,
mid(5)이하의 원소는 전부 정답범위에 들어가지 않는다.
따라서 mid값 이후 원소의 결정을 확인해야한다.
(left = mid + 1)

mid(5)의 결정이 성립하지 않았음으로,
임계값(mid) 이후의 값에 대한 결정을 확인해야한다.

left 포인터의 이동 이후,
임계값(mid) 포인터를 재조정하여 다시 결정에 대한 여부를 확인한다.

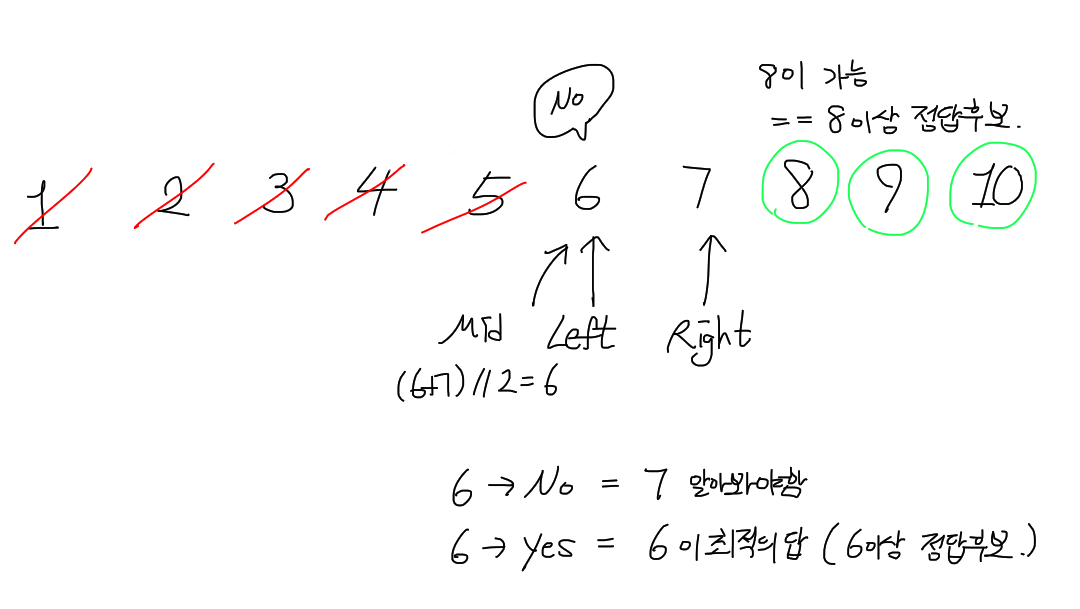
mid(8)의 결정이 성립하였음으로,
8(mid)이상의 원소들은 전부 정답 범위 안으로 들어간다.

중요한것은,
“최적화 문제”이기에 가장 최적의 결과를 찾아야한다.

따라서, 임계값을 재조정하여 앞 원소의 결정 여부를 파악한다.

다음 mid 값 (6)에 대해서
결정이 성립한다면 6이 최적의 답 일것이고
(6이상이 정답,5는 제외)
성립하지 않는다면 그 다음 임계값에 대한 결정 여부를 파악해야한다.
(7이상이 정답인가? 8이상이 정답인가?)

이와 같이 parametric search는 이분탐색법 처럼
left 포인터가 right 포인터와 만나거나 넘어갈 때까지
left,right,mid 포인터에 따라 정답을 찾는다.

다만,
큰 차이점은 결정 문제의 유무이다.
N에 대한 결정 성립으로 인한 N 이상의 정답후보.
= 연속적인 정답후보 범위 등장

이 parametric search의 시간 복잡도는 O(log N)이다.

*************************
간단하게 이론을 정리해보았고,
2805번에 대해 풀어보자면,

주어진 N개의 나무를
최소한으로 잘라 M 길이 이상의 나무를 가져가야한다.

“적어도” M 미터의 나무를 가져가기 위해,
절단기의 최대 높이를 출력한다.

이 문제를 parametric search로 접근하려면,
left 포인터를 0으로,
right 포인터를 주어진 나무의 길이 중 최대값으로,
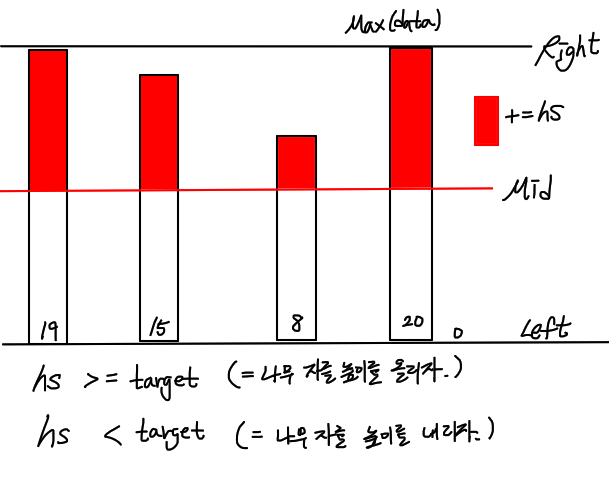
mid 값을 자르려는 나무의 길이값으로 생각해보자.

mid 값에 따라 남는 나무의 길이 합을 hs라 한다면,
이 hs 값에 대해 결정 문제를 도입하면 된다.

“적어도 M미터 보다 나무 길이가 긴가?”

아래는 python으로 작성한 코드이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import sys
N,M = map(int,sys.stdin.readline().split())
data = list(map(int,sys.stdin.readline().split()))

def binary_search(target):
    start = 0
    end = max(data) 
    while start <= end: #parametric search의 조건
        hs = 0 #가져갈 자른 나무들의 길이 합
        mid = (start + end) // 2 # mid 값 자체가 나무 자를 높이라 생각
        for i in range(len(data)): 
            if data[i] - mid > 0:   
                hs += data[i] - mid
        #자른 나무들의 길이 합을 미리 리스트에 저장하면, 시간초과가 발생함.
        #그래서 바로 반복문 안에서 mid값에 대해 자르고 남는 나무 합 가지고옴
        if hs >= target:
            temp = mid
            start = mid + 1
        # 그래서 구한 나무의 합이 구하려는 나무 합보다 크다?
        # 자를 높이를 올림 == 나무합 적어짐
        # == 최적의 자를 높이 구하기
        # 근데 그 값이 범위가 될수도 있기에 임시 저장하고
        # 마지막까지 탐색하였을 때의 temp값이 최적의 값.
        else:
            end = mid - 1
        # 구한 나무합이 구하려는 나무합보다 작으면
        # 더 밑으로 잘라야함
    return temp

print(binary_search(M))