백준 1018번 "체스판 다시 칠하기"

5 Sep 2021 ~ 22 Jul 2020

Question:

지민이는 자신의 저택에서
MN개의 단위 정사각형으로 나누어져 있는 MN 크기의 보드를 찾았다.
어떤 정사각형은 검은색으로 칠해져 있고,
나머지는 흰색으로 칠해져 있다.
지민이는 이 보드를 잘라서 88 크기의 체스판으로 만들려고 한다.

체스판은 검은색과 흰색이 번갈아서 칠해져 있어야 한다.
구체적으로,
각 칸이 검은색과 흰색 중 하나로 색칠되어 있고,
변을 공유하는 두 개의 사각형은 다른 색으로 칠해져 있어야 한다.
따라서 이 정의를 따르면 체스판을 색칠하는 경우는 두 가지뿐이다.
하나는 맨 왼쪽 위 칸이 흰색인 경우, 하나는 검은색인 경우이다.

보드가 체스판처럼 칠해져 있다는 보장이 없어서,
지민이는 88 크기의 체스판으로 잘라낸 후에
몇 개의 정사각형을 다시 칠해야겠다고 생각했다.
당연히 88 크기는 아무데서나 골라도 된다.
지민이가 다시 칠해야 하는 정사각형의 최소 개수를 구하는 프로그램을 작성하시오.

Input:

첫째 줄에 N과 M이 주어진다.
N과 M은 8보다 크거나 같고,
50보다 작거나 같은 자연수이다.
둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다.
B는 검은색이며, W는 흰색이다.

Output:

첫째 줄에 지민이가 다시 칠해야 하는 정사각형 개수의 최솟값을 출력한다.

Restriction:

시간제한:
2 초

Example Case:

Input case 1:

8 8
WBWBWBWB
BWBWBWBW
WBWBWBWB
BWBBBWBW
WBWBWBWB
BWBWBWBW
WBWBWBWB
BWBWBWBW

Output case 1:

Input case 2:

10 13
BBBBBBBBWBWBW
BBBBBBBBBWBWB
BBBBBBBBWBWBW
BBBBBBBBBWBWB
BBBBBBBBWBWBW
BBBBBBBBBWBWB
BBBBBBBBWBWBW
BBBBBBBBBWBWB
WWWWWWWWWWBWB
WWWWWWWWWWBWB

Output case 2:

풀이 과정: 이 문제는,
브루트포스 알고리즘을 활용한 문제이다.

문제를 읽어보면 대략적으로 어떻게 풀이방향을 잡아야할지 보인다.

NxM 범위의 판이 주어지고,
우리는 이 주어진 범위 내에서 무작위로 8 x 8 범위를 지정하여
검은색과 흰색으로 번갈아 가며 칠해진 체스판의 조건을 만족하는지 확인하는데,
이 조건이 만족하지 않는다면 다시 칠해야하는 정사각형 개수를 세야한다.
결과적으로 모든 범위 N x M 내 8 x 8 체스판을 찾았을 때,
다시 칠해야하는 정사각형의 개수의 최솟값을 찾아야한다.

구현부분을 생각해보면,
생각해야할 조건이 몇 가지 있다.

첫 번째로,
주어진 값이 검은색으로 첫칸이 시작한다고 해서,
검은색으로 시작하는 체스판과의
다시 칠해야하는 사각형의 최솟값은
하얀색으로 시작하는 체스판과의
다시 칠해야하는 사각형의 최솟값보다 클 수도 있다.

두 번째로,
N x M이 8 x 8 범위를 넘어가게 되면,
범위 자체를 이동 시켜야하는데,
이에 대해 어떻게 구현을 할 것 인가?

세 번째로,
범위에 대해 체스판과의 비교를 어떻게 구현할 것인가?

첫번째와 세번째에 대한 해답은,
검은색으로 시작하는 체스판과,
하얀색으로 시작하는 체스판의 배열을 따로 생성하여
이중 for문을 통해 비교하여 다르면 변수 값을 증가시킨다.
또한,
검은색-하얀색 시작 체스판 둘 다 비교하여 나온 값을
min() 함수를 사용하여 최솟값을 구해낸다.

두 번째에 대한 해답은,
범위는 8 x 8이란 고정 범위로, N x M 안에서 이동한다.
따라서,N x M 위 (i,j)라는 좌표가 존재 한다면,
이 좌표에서 부터 범위 8 x 8 안의 체스판을 비교하는 함수를 작성하여,
그에 따른 다시 칠해야하는 정사각형의 개수를 리턴한다.
그 다음,(i,j)의 좌표를 증가시켜 함수안에 다시 인자로 넣는 과정을 반복하여
범위 내 이동 및 고정 범위에 따른 최솟값 구하기가 가능하다.
참고로 시작점 i,j의 범위는 N-8 , M-8 까지이다.

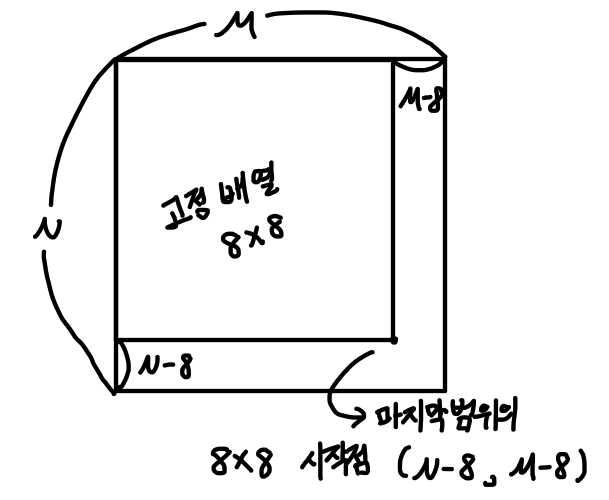
코드를 보면 이해가 될 것이다.

아래는 C++로 작성한 소스코드 이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <iostream>
#include <string>
#include <utility> //pair 헤더
#include <algorithm> //min 헤더

using namespace std;
string WB_start[8] = {
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW"
};

string BW_start[8] = {
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB"
};
string arr[50];
int WB_cnt(int x,int y) { //흰색으로 시작하는 체스판과의 비교
    int cnt = 0;
    for(int i = 0; i< 8; i++) {
        for(int j = 0; j< 8; j++) {
            if(arr[i+x][j+y] != WB_start[i][j]) { 
                //arr 배열은 이미 입력받은 배열,받은 인자값 = 변한 좌표값 => 그 좌표값부터의 8 x 8
                cnt++;
            }
        }
    }
    return cnt;
};

int BW_cnt(int x,int y) { //검은색으로 시작하는 체스판과의 비교
    int cnt = 0;
    for(int i = 0; i< 8; i++) {
        for(int j = 0; j< 8; j++) {
            if(arr[i+x][j+y] != BW_start[i][j]) {
                //arr 배열은 이미 입력받은 배열,받은 인자값 = 변한 좌표값 => 그 좌표값부터의 8 x 8
                cnt++;
            }
        }
    }
    return cnt;
}

int main() {
    int cnt;
    int mini = 121213;
    pair<int, int> p1; // pair 생성, "pair<타입1,타입2> 변수이름;"
    cin >> p1.first >> p1.second; //pair 값에 N,M 입력 받음
    for(int i = 0; i < p1.first;i++) {
        cin >> arr[i]; //arr에 값 입력
    }
    for(int i =0; i + 8 <= p1.first; i++) { // N-8 까지의 시작점 이동
        for(int j =0; j + 8 <= p1.second; j++) { // M-8까지의 시작점 이동
            int tmp;
            tmp = min(WB_cnt(i,j),BW_cnt(i,j)); // 최솟값 뽑아내기
            if(tmp < mini) {
                mini = tmp;
            }
        }
    }
    cout << mini;
    return 0;
}